

Next: The ACTION Network
Up: Simulations
Previous: The Simulation Model
The series of simulation results we carried out reflect in part the major
aim of establishing the existence of the global control model for the NRT.
In Figures 6--16, we present the results obtained from actual simulation
runs. The simulation code we developed was very modular in design, allowing
for easy scaling to more powerful simulations, which could, with some
reconfiguration, also be performed on parallel processing machines. It is
hoped in future to extend the simulations to the more realistic case of
two-dimensional sheets of thalamus, NRT and cortical tissue, and this
can easily be accommodated.
The x-axes in these plots represent the spatial positions of a line of
100 neurons. The y-axes represent 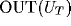 and
and 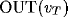 for the cases of the thalamic excitatory and inhibitory neurons respectively
(where OUT has its usual ANN interpretation), and user-scaled
for the cases of the thalamic excitatory and inhibitory neurons respectively
(where OUT has its usual ANN interpretation), and user-scaled raw
voltage output from the
raw
voltage output from the 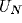 and
and 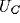 excitatory neurons in the NRT and
cortex respectively. Time delays for signal propagation between neurons were
set to zero (although they could easily be incorporated in any more realistic
future runs).
excitatory neurons in the NRT and
cortex respectively. Time delays for signal propagation between neurons were
set to zero (although they could easily be incorporated in any more realistic
future runs).
The very simplest situation one can envisage with this system is that where
there is no lateral coupling between NRT neurons. Such a system (Figure 6) is
very useful for evaluating the effect of feedback strength between neurons of
the three layers. We see that each vertical module acts in essence like an
amplifier for its particular input signal.
Since there exist a large number of free parameters in this system (between
20-60, depending on how the simulations are configured), it is useful to
determine suitable ranges for the allowed values these can take, in addition
to the constraints in (26). We do this by introducing lateral connectivity
(given by equations (14), (18)) and experimenting with different values
of the amplitudes, thresholds and temperatures of the neurons, and
the range of the spreads for the lateral terms. The last of these turns out to
be a stability parameter, in that excessively long-ranged influence of the
lateral connectivity terms leads to unrealistically large output voltages
in the NRT neurons. We identify such behaviour as the nonlinear regime of
operation.
This behaviour is illustrated in Figures 7--9,
where we successively increase
the spread from 5 to 50. Every positively valued segment of the NRT wave acts
to allow an input getting through to the cortex, while every negatively valued
segment acts to restrict it. This is best illustrated in Figure 8.
For moderate values of the spread, we find that
the spread has a second attribute as a mechanism for local control. For large
values of the spread, the NRT activity begins to grow disproportionately
(Figure 9).
The spread also plays a part in the outcome of amplitude competition, as in
Figure 10, for instance. Of the two plateaus representing strong and
weak inputs, the stronger input dominates the weaker one. The spatial
wavelengths set up in the NRT region are much smaller than the spread of
the plateaus, yet exercise strong control over the allowed cortical response.
There is partially global control over the allowed set of inputs propagating
up to the cortex, determined principally by wavelike activity in the NRT,
itself a function of the spread.
It is interesting to note here the relative effects of the difference of
Gaussian (DOG) and dendro-dendritic terms in the emergence of waves on the NRT sheet.
Figure 11 illustrates the result we obtain be eliminating the dendro-dendritic
term, while Figure 12 shows the activity upon removal of the DOG term. We
see that the DOG term is clearly less influential in both spatial waveform
generation and the development of strong patterns of activity in the cortical
layer. This is to be expected, however, since axon collaterals in the DOG
representation are not long-ranged.
The global control mechanism that is predicted in the Simplified Global ... section is illustrated in
Figures 13--16. The spatially global wave of activity on the NRT exercises wavelength
dependent control on the signals propagating forth to the cortex. The cortical
activity persisting does not reflect the inputs very strongly (Figure 14), as
it did for the partially global control in Figure 10, being influenced
instead by the oscillatory character of the NRT activity
A significant aspect of this system, when operating in a global control phase,
is its sensitive dependence on classes of inputs. We have seen that during such
a phase, the cortex only sees the winner of the competition taking place on
the NRT. Equivalently, the NRT (according to the theory of the Simplified Global ... section) is acting like
non-linear filter that allows one out of all the Fourier components presented
to it to propagate through. We expect therefore that the selection of this
particular Fourier component would be critically influenced by factors such as
the wavelength and the amplitude of the input (we noted this towards the
end of the Simplified Global ... section as well). It is difficult to establish
with certainty, however, which of these two are the more significant, since
our simulation results shows only trends in the output, and not actual
magnitudes thereof, as mentioned earlier.

Figure 6:
Simulation run with no lateral coupling between NRT neurons. The input
essentially feeds through to the cortex, as might be expected.

Figure 7:
Simulation run with lateral connectivity (both dendro-dendritic and
DOG) introduced. The value chosen for the spread is small here. Wave
activity is beginning to appear on NRT.
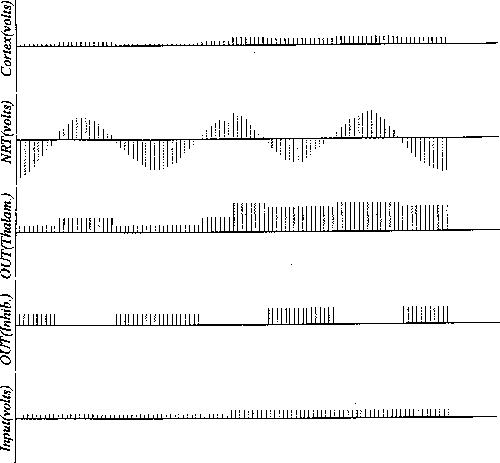
Figure 8:
As for Figure 7, but with moderate values for the spread. The NRT is
clearly influencing what is allowed to propagate through to the cortex.

Figure 9:
As for Figure 7, but with large values for the spread. The activity on
the NRT is beginning to take on a non-linear mode of operation. There
is still, however, control over what is allowed to go through to the
cortex.

Figure 10:
Simulation run showing amplitude competition. Of the strong and weak
inputs being fed in, only the strong survives the journey to the cortex.
There is partially global control exercised over this by the activity on
the NRT.
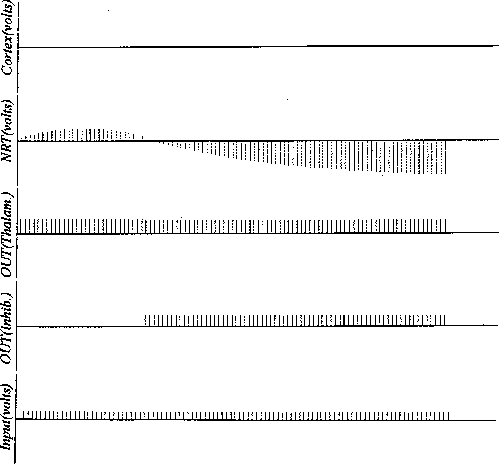
Figure 11:
Simulation run showing the development of activity on NRT with only
a DOG form for the lateral connectivity. (Compare with Figure 12).
Figure 12:
Simulation run showing the development of activity on NRT with only
a dendro-dendritic form for the lateral connectivity. (Compare with
Figure 11).

Figure 13:
Simulation run showing full global control with a spatially constant
input. The activity on the cortex reflects the activity on the NRT,
and is not dependent on the form of the input.

Figure 14:
Simulation run showing full global control with semi-constant spatial
input. Again, the cortex activity is influenced by the NRT alone.

Figure 15:
Simulation run showing full global control with short-wavelength periodic
input.
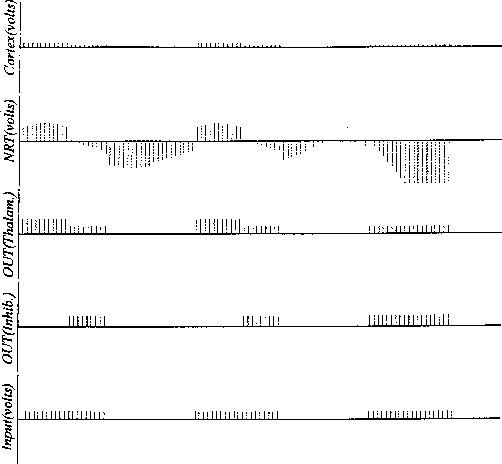
Figure 16:
Simulation run showing full global control with medium-wavelength
periodic input.


Next: The ACTION Network
Up: Simulations
Previous: The Simulation Model
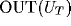 and
and 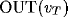 for the cases of the thalamic excitatory and inhibitory neurons respectively
(where OUT has its usual ANN interpretation), and user-scaled
for the cases of the thalamic excitatory and inhibitory neurons respectively
(where OUT has its usual ANN interpretation), and user-scaled raw
voltage output from the
raw
voltage output from the 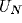 and
and 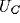 excitatory neurons in the NRT and
cortex respectively. Time delays for signal propagation between neurons were
set to zero (although they could easily be incorporated in any more realistic
future runs).
excitatory neurons in the NRT and
cortex respectively. Time delays for signal propagation between neurons were
set to zero (although they could easily be incorporated in any more realistic
future runs).










