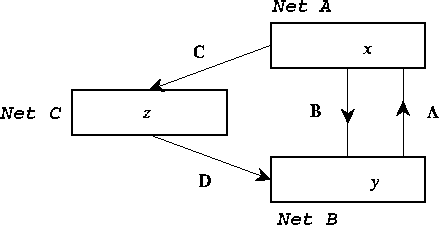
Figure 17: Schematic of the ACTION net, showing the three modules A (cortex), B (thalamus) and C (basal ganglia) with activities x, y and z respectively. The connection matrices A, B, C and D are also shown.

Figure 17:
Schematic of the ACTION net, showing the three modules A (cortex),
B (thalamus) and C (basal ganglia) with activities x, y and z
respectively. The connection matrices A, B, C and
D are also shown.
The basic structure of the ACTION network is shown in Figure 17. It
involves three interconnected modules. The first of these, denoted A
in the Figure, is the frontal cortex. This is represented as a single
module in the Figure, but is really representing any one of the set of
loops known to preserve topology on circulation of activity round the
frontal cortex  basal ganglia
basal ganglia  thalamus
thalamus
 frontal cortex [50].
The second net, B, is the region of thalamus
appropriate for the particular frontal loop considered. Finally there
is the basal ganglia C, shown in the Figure as a single layer. However
that is only a simplification for the more complex two-layered system
of which it is actually composed. The purpose of the model of the
figure is to extract the most crucial features of the more complex
structure; the disinhibitory action of the basal ganglia on the
thalamus will be preserved by the model. At the same time, there is
assumed to be lateral inhibition on the basal ganglia layer C. Thus
two of the most important features of the basal ganglia are incorporated
in the model of Figure 17.
The general connectivity being assumed between the modules of Figure 17
is topographic, with an exponential spread of a small amount. Thus the
action of the modules A and B on each other will be excitatory, as is
the feedforward action of A on C and C on B. The action of the neurons
in C on B will not be assumed adaptive, due to their having arisen from
inhibitory neurons in the globus pallidus.
frontal cortex [50].
The second net, B, is the region of thalamus
appropriate for the particular frontal loop considered. Finally there
is the basal ganglia C, shown in the Figure as a single layer. However
that is only a simplification for the more complex two-layered system
of which it is actually composed. The purpose of the model of the
figure is to extract the most crucial features of the more complex
structure; the disinhibitory action of the basal ganglia on the
thalamus will be preserved by the model. At the same time, there is
assumed to be lateral inhibition on the basal ganglia layer C. Thus
two of the most important features of the basal ganglia are incorporated
in the model of Figure 17.
The general connectivity being assumed between the modules of Figure 17
is topographic, with an exponential spread of a small amount. Thus the
action of the modules A and B on each other will be excitatory, as is
the feedforward action of A on C and C on B. The action of the neurons
in C on B will not be assumed adaptive, due to their having arisen from
inhibitory neurons in the globus pallidus.
It is assumed that the time taken for a nerve impulse to travel directly
from A to B (and vice versa) is one unit, and from A to B by way of C
to be 2n time units (so n time units for each of the passages from A
to C and C to B). In actuality, these times are respectively about 4
msec and 30 msec [40], so that n would be at least 3.
The connection matrices from B to A is denoted  , from A to B is
, from A to B is
 , from A to C,
, from A to C,  and C to B denoted
and C to B denoted  . Lateral
connection is assumed to occur on the basal ganglia, and will be denoted
by a connection matrix
. Lateral
connection is assumed to occur on the basal ganglia, and will be denoted
by a connection matrix  .
The activities of the modules A, B, C are denoted respectively by
.
The activities of the modules A, B, C are denoted respectively by  ,
,
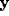 , and
, and  . The simplest equations for the development of activity
in the coupled modules are thus the update equations
. The simplest equations for the development of activity
in the coupled modules are thus the update equations
where 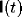 and
and 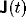 are external inputs (from heteromodal
cortex or the limbic system) arriving at the frontal cortex and basal ganglia
respectively, and the sigmoidal functions
are external inputs (from heteromodal
cortex or the limbic system) arriving at the frontal cortex and basal ganglia
respectively, and the sigmoidal functions 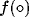 ,
, 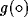 , and
, and
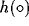 are the output
functions of the nodes A, B, and C respectively. These functions will
be assumed to have the general form
are the output
functions of the nodes A, B, and C respectively. These functions will
be assumed to have the general form 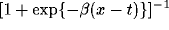 for an
activity
for an
activity  on the node in question, where t is the threshold, and
on the node in question, where t is the threshold, and
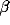 an inverse temperature. The possibility of any of these functions
being linear will
be considered later. It will be necessary to include various
extra features in order to make ACTION
have full neurobiological realism. However the first
and simplest model, that of Figure 17 and
equation (27), will hopefully
be sufficient to give a broad basis for modelling the features mentioned
earlier --- namely, active memory, comparator action, sequence
generation, and attentional control.
an inverse temperature. The possibility of any of these functions
being linear will
be considered later. It will be necessary to include various
extra features in order to make ACTION
have full neurobiological realism. However the first
and simplest model, that of Figure 17 and
equation (27), will hopefully
be sufficient to give a broad basis for modelling the features mentioned
earlier --- namely, active memory, comparator action, sequence
generation, and attentional control.
There is now the question of determining the nature of the response of
the system (27) to the inputs I and J. There are a large range of nets
specified by this structure, since there is a great choice of the
connection matrices 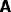 ,
, 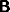 ,
, 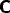 ,
, 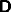 ,
, 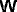 and
and  .
The interconnectivity between
the different modules has been assumed to be topographic, so that each
of the corresponding connection matrices
.
The interconnectivity between
the different modules has been assumed to be topographic, so that each
of the corresponding connection matrices
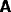 ,
, 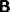 ,
, 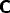 and
and 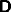 will be assumed to be nearly
diagonal. It is clear that the lateral connection matrices are not of
that form. They will be considered in more detail later, but will
initially be neglected.
will be assumed to be nearly
diagonal. It is clear that the lateral connection matrices are not of
that form. They will be considered in more detail later, but will
initially be neglected.
An important question, not contained explicitly in the ACTION network assumptions outlined above, is that of the coding of information by the networks concerned. The most accessible of these seems to be for cortex, where there is known topographic representations of the body in the motor cortex. In that case, it seems that locally there is a population vector coding [20], in which there is a random distribution of preferred vectors for movement of a local region. The scale of the modelling in ACTION is such that only the population vector is observable, so such a randomisation will not be necessary. In any case, the lateral spread of the connection matrices should not cause problems of continued looping of activity by such randomisations.