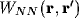 on the R.H.S.
of (11). The former of these gives (assuming symmetry in the x and y
directions)
on the R.H.S.
of (11). The former of these gives (assuming symmetry in the x and y
directions)
The model of Figure 2, expressed mathematically by equations (10)--(15), is expected to have similar properties to those of the various models associated with Figure 1 and discussed in the Simplified Global ... section. That is clear for the asymptotic solutions satisfying the equations obtained by setting the left hand sides of (10)--(15) all to zero. The main differences between this static system and the earlier equations of are:
(i) the presence of the C-layer and its feedback,
(ii) non-linearity of all neurons,
(iii) the presence of the inhibitory interneurons IN, and NRT feedback to them rather than the T-cells (as in Figure 1).
We will briefly discuss each of these features in turn.
The cortical layer can be seen as a mechanism for achieving extra input amplification, by means of the thalamus-cortex-thalamus feedback loop, as has already been discussed by La Berge and colleagues [33]. This amplification may make the competition on NRT more effective [33]. This will be borne out by simulation of our complete system. Non-trivial transforms in C will be expected to modify this result, but will not be considered here.
The non-linear functionality of neurons was already argued to be a means of increasing the sensitivity of the system in the Simplified Global ... section. We will appeal to this same argument here.
The inhibitory interneurons have been included so as to be able to implement Dale's Law properly. This is clearly satisfied in Figure 2 and equations (22)--(25). The effect of NRT activity on the IN cells will therefore be that of disinhibition, which is a mode of action used in numerous parts of the brain. Its net effect, for suitable parameter ranges of cell thresholds is similar to that of excitation of NRT activity directly on the thalamic relay cells, as observed experimentally for example by Steriade et al. [41]. In this range of parameters, then, the disinhibitory NRT-IN-T activity of Figure 2 reduces to the net excitatory NRT-T activity of Figure 1.
It would appear that the model of Figure 2 should therefore have similar properties to that of Figure 1, in particular supporting both local and global competition and being able to account for endogenous activity by addition of direct input to NRT on the R.H.S. of (11). However, there is still the crucial question of stability and more detailed input-dependence, of plane waves excited globally across the NRT.
Stability can be analysed by looking at higher order terms that might
arise in (15), and also consider a linearised analysis of the lateral connection
term involving the connection weight 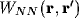 on the R.H.S.
of (11). The former of these gives (assuming symmetry in the x and y
directions)
on the R.H.S.
of (11). The former of these gives (assuming symmetry in the x and y
directions)
and the latter, for a Gaussian spread of lateral inhibition, the convolution product
where
with b<a. The dispersion relation for the temporal dependence 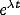 of the NRT membrane potential in (11), neglecting all but the lateral
connections as a first approximation (since the other terms do not play
a crucial role) becomes for the Fourier mode
of the NRT membrane potential in (11), neglecting all but the lateral
connections as a first approximation (since the other terms do not play
a crucial role) becomes for the Fourier mode 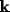 ,
,
with
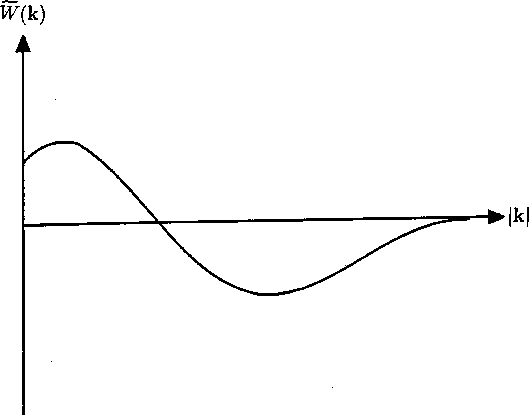
Figure 3:
Dependence of the Fourier transform
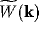 of the lateral NRT connection weights on the wave
variable k. Initially positive, the value of becomes negative, so
producing possible instability according to equation (19).
of the lateral NRT connection weights on the wave
variable k. Initially positive, the value of becomes negative, so
producing possible instability according to equation (19).
Figure 4:
Dispersion relation for 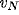 in
wave-number space. The interval
in
wave-number space. The interval 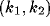 contains the wave number
for which instability occurs, and spatially inhomogeneous activity is
expected to arise.
contains the wave number
for which instability occurs, and spatially inhomogeneous activity is
expected to arise.
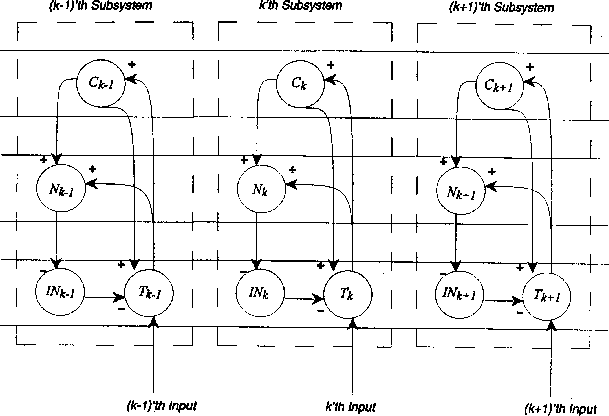
Figure 5:
Schematic of the ``modularised'' version of Figure 2, as used in
obtaining the results of the computer simulations.
In Figure 3, the general shape of 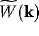 is plotted, and in
Figure 4, that of
is plotted, and in
Figure 4, that of 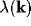 . Instability arises for values of
. Instability arises for values of
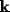 for which
for which 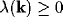 . This is the interval
. This is the interval 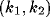 in
Figure 4.
As argued with clarity in Murray [38], inhomogeneous NRT activity, with wave
numbers in the interval
in
Figure 4.
As argued with clarity in Murray [38], inhomogeneous NRT activity, with wave
numbers in the interval 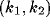 will be expected to grow. The stability
of the resulting globally inhomogeneous activity depends on the more detailed
non-linear system (10)--(14), and presently can only be ascertained by simulation.
Results of the latter will be presented in the Simulations section; they will show the system is
stable. The dependence of the winning activity on the maximum of the wave-length
number being singled out by the competition on NRT will be discussed
further in the Simulations section.
will be expected to grow. The stability
of the resulting globally inhomogeneous activity depends on the more detailed
non-linear system (10)--(14), and presently can only be ascertained by simulation.
Results of the latter will be presented in the Simulations section; they will show the system is
stable. The dependence of the winning activity on the maximum of the wave-length
number being singled out by the competition on NRT will be discussed
further in the Simulations section.
There is finally the non-trivial dependence on the inputs of the inhomogeneous mode winning the competition on the NRT sheet. Thus, whilst equation (19) would seem to indicate lack of dependence of this mode on the input, the full non-linear system does indeed have such a dependence. There does not seem to be much mathematical analysis of this problem in the literature, although dependence on boundary and initial conditions for reaction-diffusion models has been studied [3]. We will turn to answer this question by simulation in the Simulations section.