

Next: Dynamic Receptive Fields
Up: Self-Organization of Orientation Maps
Previous: The Receptive Field
The model consisted of an array of 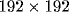 neurons, and a
retina of
neurons, and a
retina of 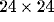 receptors. The anatomical receptive field of
each neuron covered
receptors. The anatomical receptive field of
each neuron covered 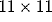 receptors. The initial lateral
excitation radius was 19 and was gradually decreased to 1. The
lateral inhibitory radius of each neuron was 47, and weak inhibitory
connections were pruned away at intervals of 10,000 iterations.
receptors. The initial lateral
excitation radius was 19 and was gradually decreased to 1. The
lateral inhibitory radius of each neuron was 47, and weak inhibitory
connections were pruned away at intervals of 10,000 iterations. The
network had approximately 400 million connections in total, took 10
hours to simulate on 64 processors of the Cray T3D at the Pittsburgh Supercomputing Center.
The
network had approximately 400 million connections in total, took 10
hours to simulate on 64 processors of the Cray T3D at the Pittsburgh Supercomputing Center.
The self-organization of afferents results in a variety of
oriented RFs similar to those found in the visual cortex (figure
2). Some are highly selective
to inputs of a particular orientation, others unselective.
The global organization of such receptive fields can be visualized
by labeling each neuron by the preferred angle and degree of selectivity
to inputs at that angle. The resulting orientation map
(figure 3; movie 1)
is remarkably similar in structure to those observed in the primary
visual cortex by recent imaging techniques
[6,7]
and contains structures such as pinwheels, fractures and
linear zones. The results strongly suggest that Hebbian self-organization of afferent
weights, based on recurrent lateral interactions, underlie
the development of orientation maps in the cortex.
The results strongly suggest that Hebbian self-organization of afferent
weights, based on recurrent lateral interactions, underlie
the development of orientation maps in the cortex.
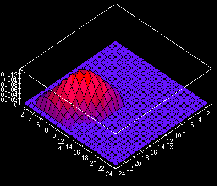 |
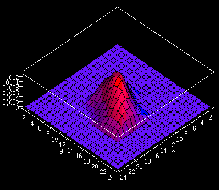 |
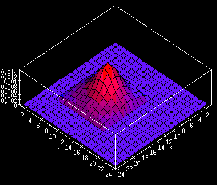 |
(a) RF shaprly tuned to 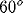 |
(b) RF shaprly tuned to 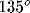 |
(c) Unselective RF |
Figure 2:
(click on the image to view a larger version)
Self-organization of oriented afferent receptive fields. The afferent
weights of three neurons at different locations in the network
are shown, plotted on the retinal surface.
The first two are strongly oriented, whereas the third is unoriented
and symmetric.
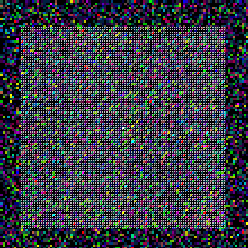 |
 |
 |
| (a) Initial unordered map and connections |
(b) Final oriented map and connections |
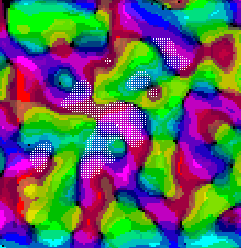
Figure 3: (click on the image to view a larger version) Self-organization of
the orientation map and lateral connections. Each neuron in this  central region of the map is colored by
the orientation preference of its afferent weights, as illustrated by
the color bar. Colors varying between red
central region of the map is colored by
the orientation preference of its afferent weights, as illustrated by
the color bar. Colors varying between red 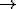 magenta
magenta 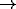 blue
blue 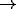 green
green
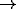 orange represent continuously-changing eye
preference from 0 to 180 degrees. The brightness of the color
indicates how selective the receptive field is to its preferred
orientation. (a) Initially, the
afferent weights of each neuron are random, and the receptive fields are
randomly oriented and are mostly unselective (indicated by the dim
colors). (b)
After several thousand input presentations, the receptive fields
organize into continuous and highly selective (brightly colored) bands
of orientation columns, and only lateral connections between similar
orientation columns remain. The orientation sensitivity patterns have
all the significant features of primary visuo-cortical maps, as observed
by techniques such as voltage-sensitive dye imaging
[6,7]: (1) pinwheel
centers, around which orientation preference changes through
orange represent continuously-changing eye
preference from 0 to 180 degrees. The brightness of the color
indicates how selective the receptive field is to its preferred
orientation. (a) Initially, the
afferent weights of each neuron are random, and the receptive fields are
randomly oriented and are mostly unselective (indicated by the dim
colors). (b)
After several thousand input presentations, the receptive fields
organize into continuous and highly selective (brightly colored) bands
of orientation columns, and only lateral connections between similar
orientation columns remain. The orientation sensitivity patterns have
all the significant features of primary visuo-cortical maps, as observed
by techniques such as voltage-sensitive dye imaging
[6,7]: (1) pinwheel
centers, around which orientation preference changes through 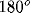 ,
seen as a color wheel from red to blue to orange, (2) linear
zones, where orientation preference changes almost linearly, seen as a
rainbow-like patch with all colors, and (3) fractures, where there
is a discontinuous change of orientation preference (e.g. locations
where colors change rapidly from magenta to green or magenta to
yellow). In addition to the orientation preference and selectivity, the
figures also display the lateral connections of one particular neuron on
the map. The small white dots indicate neurons from which the neuron
marked with the big white dot receives lateral input. (a)
Initially, the lateral connections are uniform and widespread.
(b) After pruning, only connections between similar orientation columns
remain. The marked neuron is colored magenta, and its connections come
mostly from magenta and blue neurons.
In the near vicinity, the lateral connections follow the twists and
turns of the magenta-colored iso-orientation column. The magenta color
represents an orientation of 60 degrees, and the lateral connections
are elongated along this direction.
,
seen as a color wheel from red to blue to orange, (2) linear
zones, where orientation preference changes almost linearly, seen as a
rainbow-like patch with all colors, and (3) fractures, where there
is a discontinuous change of orientation preference (e.g. locations
where colors change rapidly from magenta to green or magenta to
yellow). In addition to the orientation preference and selectivity, the
figures also display the lateral connections of one particular neuron on
the map. The small white dots indicate neurons from which the neuron
marked with the big white dot receives lateral input. (a)
Initially, the lateral connections are uniform and widespread.
(b) After pruning, only connections between similar orientation columns
remain. The marked neuron is colored magenta, and its connections come
mostly from magenta and blue neurons.
In the near vicinity, the lateral connections follow the twists and
turns of the magenta-colored iso-orientation column. The magenta color
represents an orientation of 60 degrees, and the lateral connections
are elongated along this direction.
Movie 1
(small (348K) and large (958K)):
Self-Organization of the Orientation Map. Starting from initially random
orientation preferences and low selectivity (indicated by the dark
colors), the map gradually develops more selectivity, and the
preferences become globally ordered over the course of 35,000 presentations. The
frames were taken in approximately exponentially increasing intervals,
with 10 presentations between frames in the beginning, and increasing
to 2500 presentations between frames in the end of the simulation.
The lateral connection weights self-organize at the same time as the
orientation map forms. Initially, the connections are spread over long
distances and cover a substantial part of the network
(figure 3 a). As lateral weights self-organize, the
connections between uncorrelated regions grow weaker, and after pruning,
only the strongest connections remain (figure 3
b). The surviving connections of highly-tuned cells, such as the one
illustrated in figure 3 b, link areas of similar
orientation preference, and avoid neurons with the orthogonal
orientation preference. Furthermore, the connection patterns are
elongated along the direction that corresponds to the neuron's preferred
stimulus orientation. This organization reflects the activity
correlations caused by the elongated Gaussian input pattern: such a
stimulus activates primarily those neurons that are tuned to the same
orientation as the stimulus, and located along its length. At locations
such as fractures, where a cell is sandwiched between two orientation
columns of very different orientation preference, the lateral
connections are elongated along the two directions preferred by the two
adjacent columns (figure 4 a). Finally, the lateral
connections of unselective cells, such as those at pinwheel centers,
connect to all orientations around the cell (figure 4
b). Thus the pattern of lateral connections of each neuron closely
follows the global organization of receptive fields, and represents the
long-term activity correlations over large areas of the network.
 |
 |
 |
| (a) Connections at fractures |
(b) Connections at pinwheels |
Figure 4: (click on the image to view a larger version)
Lateral connections at fractures and pinwheels.
Two subareas of the orientation map of figure 3 b are shown enlarged
here. The connections of neurons at fractures are typically elongated
along two directions, corresponding to the orientation preferences of
the neighboring columns. However, at pinwheel centers, the lateral
connections come from all orientations and are more or less isotropic.
Some of these results have already been
confirmed in very recent neurobiological experiments  [13].
In the iso-orientation columns
of the tree-shrew cortex, horizontal connections were found
to be distributed anisotropically, extending farther and giving rise
to more terminals along the preferred orientation of the neuron.
Most
of these terminals also connected to cells with the same orientation
preference. The connection patterns at pinwheel
centers and fractures have not been studied experimentally so far;
our model predicts that they will have unselective and biaxial
distributions, respectively.
[13].
In the iso-orientation columns
of the tree-shrew cortex, horizontal connections were found
to be distributed anisotropically, extending farther and giving rise
to more terminals along the preferred orientation of the neuron.
Most
of these terminals also connected to cells with the same orientation
preference. The connection patterns at pinwheel
centers and fractures have not been studied experimentally so far;
our model predicts that they will have unselective and biaxial
distributions, respectively.
So far this article has focused on how the model can give a
computational explanation for a number of observed structures in the
visual cortex, and how it can predict others. In related work,
we have also shown how patterns of
ocular dominance and lateral connections can self-organize cooperatively,
and how their periodicity varies with between-eye
correlations
[40,41,42].
The model can also be used to study dynamic phenomena in the
adult cortex. One such study analyzed how the
network reorganizes in response to cortical lesions and intracortical
microstimulation [39].
The phenomenon of dynamic receptive fields, which has captured
much scientific attention recently, can also be given a computational
account, as will be described below.


Next: Dynamic Receptive Fields
Up: Self-Organization of Orientation Maps
Previous: The Receptive Field
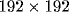 neurons, and a
retina of
neurons, and a
retina of 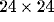 receptors. The anatomical receptive field of
each neuron covered
receptors. The anatomical receptive field of
each neuron covered 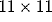 receptors. The initial lateral
excitation radius was 19 and was gradually decreased to 1. The
lateral inhibitory radius of each neuron was 47, and weak inhibitory
connections were pruned away at intervals of 10,000 iterations.
receptors. The initial lateral
excitation radius was 19 and was gradually decreased to 1. The
lateral inhibitory radius of each neuron was 47, and weak inhibitory
connections were pruned away at intervals of 10,000 iterations. The
network had approximately 400 million connections in total, took 10
hours to simulate on 64 processors of the Cray T3D at the Pittsburgh Supercomputing Center.
The
network had approximately 400 million connections in total, took 10
hours to simulate on 64 processors of the Cray T3D at the Pittsburgh Supercomputing Center.





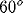
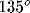
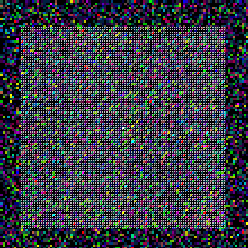


 central region of the map is colored by
the orientation preference of its afferent weights, as illustrated by
the color bar. Colors varying between red
central region of the map is colored by
the orientation preference of its afferent weights, as illustrated by
the color bar. Colors varying between red  magenta
magenta  blue
blue 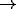 green
green
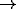 orange represent continuously-changing eye
preference from 0 to 180 degrees. The brightness of the color
indicates how selective the receptive field is to its preferred
orientation. (a) Initially, the
afferent weights of each neuron are random, and the receptive fields are
randomly oriented and are mostly unselective (indicated by the dim
colors). (b)
After several thousand input presentations, the receptive fields
organize into continuous and highly selective (brightly colored) bands
of orientation columns, and only lateral connections between similar
orientation columns remain. The orientation sensitivity patterns have
all the significant features of primary visuo-cortical maps, as observed
by techniques such as voltage-sensitive dye imaging
[6,7]: (1) pinwheel
centers, around which orientation preference changes through
orange represent continuously-changing eye
preference from 0 to 180 degrees. The brightness of the color
indicates how selective the receptive field is to its preferred
orientation. (a) Initially, the
afferent weights of each neuron are random, and the receptive fields are
randomly oriented and are mostly unselective (indicated by the dim
colors). (b)
After several thousand input presentations, the receptive fields
organize into continuous and highly selective (brightly colored) bands
of orientation columns, and only lateral connections between similar
orientation columns remain. The orientation sensitivity patterns have
all the significant features of primary visuo-cortical maps, as observed
by techniques such as voltage-sensitive dye imaging
[6,7]: (1) pinwheel
centers, around which orientation preference changes through 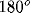 ,
seen as a color wheel from red to blue to orange, (2) linear
zones, where orientation preference changes almost linearly, seen as a
rainbow-like patch with all colors, and (3) fractures, where there
is a discontinuous change of orientation preference (e.g. locations
where colors change rapidly from magenta to green or magenta to
yellow). In addition to the orientation preference and selectivity, the
figures also display the lateral connections of one particular neuron on
the map. The small white dots indicate neurons from which the neuron
marked with the big white dot receives lateral input. (a)
Initially, the lateral connections are uniform and widespread.
(b) After pruning, only connections between similar orientation columns
remain. The marked neuron is colored magenta, and its connections come
mostly from magenta and blue neurons.
In the near vicinity, the lateral connections follow the twists and
turns of the magenta-colored iso-orientation column. The magenta color
represents an orientation of 60 degrees, and the lateral connections
are elongated along this direction.
,
seen as a color wheel from red to blue to orange, (2) linear
zones, where orientation preference changes almost linearly, seen as a
rainbow-like patch with all colors, and (3) fractures, where there
is a discontinuous change of orientation preference (e.g. locations
where colors change rapidly from magenta to green or magenta to
yellow). In addition to the orientation preference and selectivity, the
figures also display the lateral connections of one particular neuron on
the map. The small white dots indicate neurons from which the neuron
marked with the big white dot receives lateral input. (a)
Initially, the lateral connections are uniform and widespread.
(b) After pruning, only connections between similar orientation columns
remain. The marked neuron is colored magenta, and its connections come
mostly from magenta and blue neurons.
In the near vicinity, the lateral connections follow the twists and
turns of the magenta-colored iso-orientation column. The magenta color
represents an orientation of 60 degrees, and the lateral connections
are elongated along this direction.

