The extent of receptive fields and the degree of initial order in undeveloped cortical networks have not been characterized in great detail. There are three possibilities:
The three networks were simulated with Gaussian spots of ``light'' on
the retina as input. At each presentation, the activation
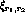at the receptor 
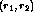was given by:
where n is the number of spots,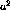 
specifies the width of the
Gaussian, and the spot centers (
,
): 
,
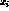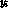were chosen randomly.
When the networks were trained with single light spots (n=1), similar afferent and lateral connection structures developed in all three cases. With more realistic input consisting of multiple light spots (n>1), the first and the third network self-organized just as robustly. Figures 2-4 illustrate the self-organization of the first network. The initial rough pattern of afferent weights of each neuron evolved into a hill-shaped profile (figure 2). The afferent weight profiles of different neurons peaked over different parts of the retina, and their center of gravities (calculated in retinal coordinates) formed a topographical map (figure 3).
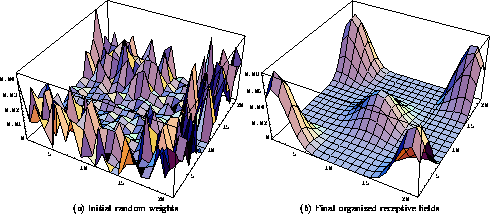
Figure 2: Self-organization of
the afferent input weights. The afferent weights
of five neurons (located at the center and at the four corners of the
network) are superimposed on the retinal surface in this figure. The
retina had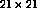 
receptors, and the receptive field radius was
chosen to be 8. Therefore, neurons could have anywhere from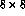 
to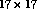 
afferents depending on their distance from the
network boundary. ( a) The anatomical RF centers were
topographically ordered, and the weights were
initialized randomly. There are four concentrated areas of
weights slightly displaced from the corners, and one larger one in the
middle. At the corners, the profiles are taller because the
normalization divides the total afferent weight among a smaller numer of
connections. ( b) As the self-organization progresses,
the weights organize into smooth hill-shaped profiles. In this simulation,
each input consisted of 3 randomly-located Gaussian spots with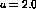 
.
The lateral interaction strengths were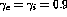 
, with
total lateral excitation = total inhibition =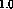 
. The learning rates
were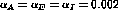 
, and the upper and lower thresholds
of the sigmoid were 0.65 and 0.1 respectively. Only the parameters
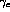and the sigmoid's upper threshold were somewhat sensitive.
CLICK TO SEE FULL-SIZE FIGURE: 
Figure 3: Self-organization of
scattered receptive fields into a topographic map. The center of
gravity of the afferent weight vector of each neuron in the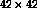 
network is projected onto the receptive surface (represented by the
square). Each center of gravity point is connected to those of the four
immediately neighboring neurons by a line. The resulting dark grid
depicts the topographical organization of the map. In (a), the
anatomical RF centers were topographically
ordered, but because the afferent weights were initially random, the
center of gravities are locally scattered. As the
self-organization progresses, the map unfolds and the weight vectors
spread out to form a regular topographic map of the receptive surface,
such as shown in ( b). The self-organization is robust with
single- and multi-spot inputs.
With multi-spot inputs, the second network failed to develop global order. It is interesting to analyze why. With single light spots, the afferent weights of an active neuron always change towards a single, local input pattern. Eventually these weights become concentrated around a local area in the RF such that the global distribution of the centers best approximates the input distribution. However, when multiple spots occur in the receptive field at the same time, the weights change towards several different locations. Since the spots are uniformly distributed, these changes cancel over time, and the weights end up concentrated somewhere around the center of the anatomical RF. If the RF centers are already ordered, this process will simply refine the already existing topographic map; if the anatomical RF centers cross, the weight centers will stay crossed. On the other hand, in the third case (of extremely large receptive fields), all neurons see essentially the same input patterns, and develop into a map of the input space as in the standard self-organizing map. The model therefore predicts that the initial afferent connections to the undeveloped cortex must either cover almost the entire retina, or the receptive field centers must be initially ordered.
The lateral connections evolve together with the afferents. By the normalized Hebbian rule (equation 3), the lateral connection weights of each neuron are distributed according to how well the neuron's activity correlates with the activities of the other neurons. As the afferent receptive fields organize into a uniform map (figure 3), these correlations fall off with distance approximately like a Gaussian, with strong correlations to near neighbors and weaker correlations to more distant neurons. The lateral excitatory and inhibitory connections acquire the Gaussian shape, and the combined lateral excitation and inhibition becomes an approximate difference of Gaussians (or a ``Mexican hat''; figure 4).
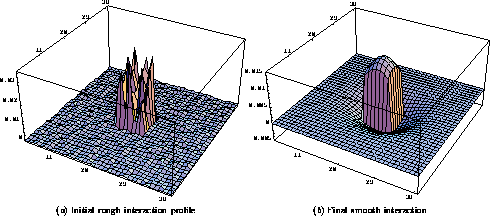
Figure 4: Self-organization of
the lateral interaction. The lateral interaction profile for a neuron
at position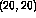 
in the 
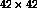network is plotted. The
excitation and inhibition weights are initially randomly distributed
within radii 3 and 18. The combined interaction is the sum of the
excitatory and inhibitory weights and illustrates the total effect of
the lateral connections. The sums of excitation and inhibition were
chosen to be equal, but because there are fewer excitatory connections,
the interaction has the shape of a rough plateau with a central peak
( a). During self-organization, smooth patterns of excitatory and
inhibitory weights evolve, resulting in a smooth ``Mexican hat'' shaped
lateral interaction profile ( b).
The activity patterns in cortical networks are not uniformly random as in the above experiments-the visual cortex, for example, has a rich structure of orientation and ocular dominance columns which restricts the type of activity patterns that can occur. As a first step to studying how lateral connections evolve in the visual cortex, the development of ocular dominance was simulated. A second retina was added to the model and afferent connections were set up exactly as for the first retina (with local receptive fields and topographically ordered RF centers). Multiple Gaussian spots were presented in each eye as input, with no between-eye correlations (as in strabismus). Because of cooperation and competition between inputs from the two eyes, groups of neurons developed strong afferent connections to one eye or the other, resulting in patterns of ocular dominance in the network (cf. [19,11]).
As figure 5 illustrates, the final lateral connection patterns closely follow the ocular dominance organization. As neurons become better tuned to one eye or the other, activity correlations between regions tuned to the same eye become stronger, and correlations between opposite eye areas weaker. As a result, monocular neurons develop strong lateral connections to regions with the same eye preference, and weak connections to regions of opposite eye preference. Most neurons are monocular, but a few binocular neurons occur at the boundaries of ocular dominance regions. Because they are equally tuned to the two eyes, the binocular neurons have activity correlations with both ocular dominance regions, and their lateral connection weights are distributed more or less equally between them. The lateral connections thus represent the simple Gestalt rule that under strabismus, the significant visual correlations are between monocular regions.
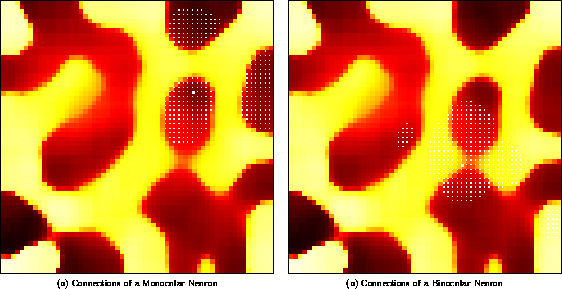
Figure 5: Patterned long-range lateral connections
in an ocular dominance model. Each neuron is colored with a color
value ( black 
orange 
white)
that represents
continuously changing eye preference from exclusive left through
binocular to exclusive right. Small blue dots indicate the strongest
lateral input connections to the neuron marked with a big blue dot.
( a) The lateral connections of a left monocular neuron
predominantly link areas of the same ocular dominance. ( b) The
lateral connections of a binocular neuron come from both eye regions.
The lateral connection patterns shown above closely match observations in the primary visual cortex. When between-eye correlations are abolished in kittens by surgically induced strabismus, long-range lateral connections primarily link areas of the same ocular dominance [9]. However, binocular neurons, located between ocular dominance columns, retained connections to both eye regions. The receptive field model confirms that such patterned lateral connections develop based on correlated neuronal activity, and demonstrates that they can self-organize simultaneously with ocular dominance columns. The model also predicts that the long-range connections have an inhibitory function.
