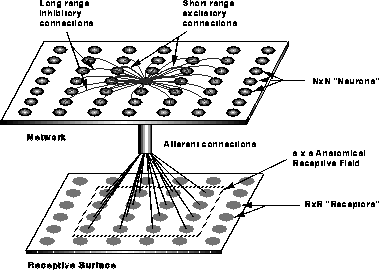
Figure 1: The Receptive-Field
LISSOM architecture. The afferent and lateral connections of a single
neuron in the network are shown. All connection weights are positive.
The cortical network is modeled as a sheet of neurons interconnected
by short-range excitatory lateral connections and long-range inhibitory
lateral connections (figure 1). Neurons receive input
from a receptive surface or ``retina'' through the afferent connections.
These connections come from overlapping patches on the
retina called anatomical receptive fields, or RFs. The
patches are distributed with a given degree of randomness. The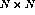 
network is projected on the retina of 
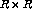receptors,
and each neuron is assigned a receptive field center 
randomly within a radius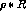 
(
)
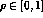of the neuron's projection.
Through the afferent connections, the neuron receives input from receptors
in a square area around the center with side s. Depending on its
location, the number of afferents to a neuron could vary from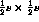 
(at the corners) to 
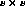(at the center).
The external and lateral weights are organized through an
unsupervised learning process. At each training step, neurons start out
with zero activity. The initial response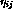 
of neuron 
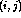is based on the scalar product
where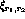 
is the activation of a retinal receptor
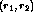within the receptive field of the neuron, 
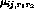is
the corresponding afferent weight, and 
is a piecewise linear
approximation of the familiar sigmoid activation function.
The response
evolves over time through lateral interactions. At each time step, the
neuron combines retinal activation with lateral excitation and
inhibition:
where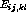 
is the excitatory lateral connection weight on the
connection from neuron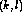 
to neuron 
, 
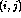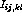is the
inhibitory connection weight, and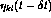 
is the
activity of neuron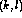 
during the previous time step. The constants
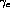and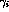 
are scaling factors on the excitatory and
inhibitory weights and determine the strength of the lateral
interactions. The activity pattern starts out diffuse and spread over a
substantial part of the map, but within a few iterations (of
equation 2), converges into a stable focused patch of
activity, or activity bubble. After the activity has settled, the
connection weights of each neuron are modified. Both afferent and
lateral connection weights adapt according to the same mechanism: the
Hebb rule, normalized so that the sum of the weights is constant:
where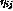 
stands for the activity of the neuron 
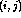in the
settled activity bubble,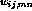 
is the afferent or the lateral
connection weight (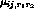
, 
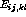or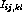 
),
is the learning rate for each type of connection (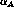
for afferent weights, 
for excitatory, and 
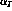for
inhibitory) and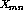 
is the presynaptic activity (
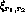for afferent, 
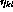for lateral). Afferent inputs, lateral excitatory
inputs, and lateral inhibitory inputs are normalized separately.
The larger the product of the
pre- and post-synaptic activity 
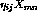, the larger the
weight change. Therefore, connections between areas with correlated
activity are strengthened the most; normalization then redistributes the
changes so that the sum of each weight type for each neuron remains
constant.
