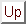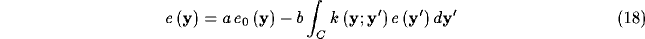
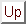
From (10), the distribution of excitation on the cortical plane can be explicitly rewritten as
where, see equations (9) and (11)
According to the method of Fredholm for inhomogeneous integral equations [121] an approximate solution of equation (18) can be expressed in the form
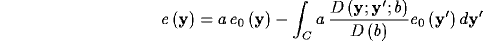
where
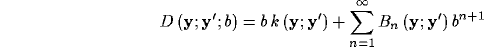
Substituting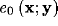 
from (19)
and
comparing the result with (8) we identify the kernel
and thence the resulting RF 
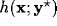after
recurrent inhibition:
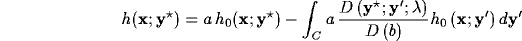
Making explicit the parametric mapping between cortical plane (C) and visual field (S), the resulting RF can be formulated as
where
is the equivalent inhibitory kernel in the feed-forward form.
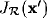denotes the Jacobian
of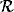 
and the absolute value of its determinant is the local
magnification factor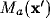 
of the mapping 
.
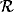A more detailed derivation of this solution can be found in the Appendix.
