

Next: The resultant receptive
Up: Linear analysis of
Previous: Superposition Assumption
The arbors of most interneurons are confined to laterally restricted
circular areas of 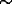 200:300
200:300 [73,104], thus leading to an
inhibitory action which is strongly local and uniformly distributed on the
horizontal plane. Such local inhibitory circuits are mainly involved in the
regulation of the gain of excitatory input
[32,33]. Much more interesting, for its functional implications, is long-range inhibition, evoked, often along
preferred directions, by clustered locations on the cortical surface.
The origin of this kind of inhibition can be related to
disynaptic activation of locally confined inhibitory interneurons through
long-range clustered branches of pyramidal cells
[81,94], and to the monosynaptic inhibitory action of basket cells which also have relatively long clustered axon collaterals, elongated in particular
directions and running tangentially for up to a millimeter from the soma
[63,64,65,67,104]. To model the consequences of this long-range inhibition, the kernel
[73,104], thus leading to an
inhibitory action which is strongly local and uniformly distributed on the
horizontal plane. Such local inhibitory circuits are mainly involved in the
regulation of the gain of excitatory input
[32,33]. Much more interesting, for its functional implications, is long-range inhibition, evoked, often along
preferred directions, by clustered locations on the cortical surface.
The origin of this kind of inhibition can be related to
disynaptic activation of locally confined inhibitory interneurons through
long-range clustered branches of pyramidal cells
[81,94], and to the monosynaptic inhibitory action of basket cells which also have relatively long clustered axon collaterals, elongated in particular
directions and running tangentially for up to a millimeter from the soma
[63,64,65,67,104]. To model the consequences of this long-range inhibition, the kernel 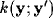 presents significant values only at a certain distance from
their centers, and along a direction forming a specific angle
presents significant values only at a certain distance from
their centers, and along a direction forming a specific angle 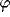 with
the horizontal axis.
with
the horizontal axis.
In the simplest case, we model such kernel as the sum of two weighted offset
circular Gaussians, that are displaced symmetrically with
respect to the location on the cortical plane they are referred to.
For an horizontal displacement (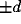 ) the kernel will be
) the kernel will be
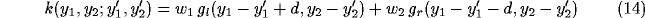
where the g's are Gaussian functions
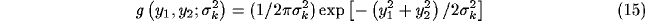
and the w's are weights.
For a displacement (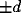 ) along a direction
) along a direction  the kernel will be
the kernel will be
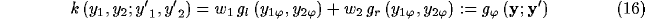
where
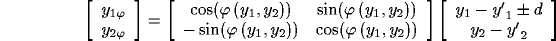
with the - sign for 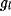 and the + sign for
and the + sign for 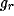 .
.
The width of the Gaussians 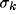 and their offset d are such that no
connections are established between two cells when their intracortical distance
is either too large or too small.
Moreover, the lateral spreading of interconnections can be characterized by
the angular bandwidth
and their offset d are such that no
connections are established between two cells when their intracortical distance
is either too large or too small.
Moreover, the lateral spreading of interconnections can be characterized by
the angular bandwidth 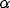 related to the half peak magnitude extension
of the kernel
related to the half peak magnitude extension
of the kernel
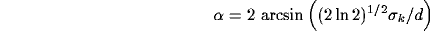
This relation implies that we cannot change the angular spread of
inhibition without affecting also its spatial localization. To overcome
this limitation, we define generalized kernels
by summing up equal circular Gaussians whose centers are uniformly spaced on
the arc of circumference with radius d under the span angle 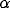 (see
figure 2).
(see
figure 2).
In this way, the inhibitory kernel becomes:
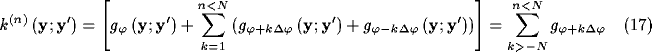
where 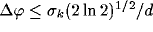 ,
,
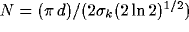 .
In this case the angular bandwidth results:
.
In this case the angular bandwidth results:
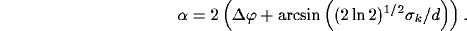
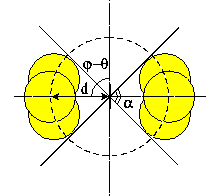
Figure 2: (click on the image to view a larger version)
Example of a typical inhibitory kernel 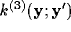 with
with 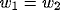 ,
, 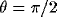 ,
, 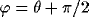 ,
, 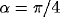 .
(a) 2D plot of the kernel. (b) Schematic representation of the spatial
extension of connections; the vertical thick line in the center
represents the orientation of the target cell. (c) Schematic mode of
operation on the
cortical plane: the marked cell (thick line) receives inhibition from
the cells (thin lines) in the shaded area.
.
(a) 2D plot of the kernel. (b) Schematic representation of the spatial
extension of connections; the vertical thick line in the center
represents the orientation of the target cell. (c) Schematic mode of
operation on the
cortical plane: the marked cell (thick line) receives inhibition from
the cells (thin lines) in the shaded area.
Since we are mainly interested in the
organization of the RFs along their cross-orientation axis
(i.e., the axis orthogonal to the RF orientation), we dwell mainly
upon those axon fields that extend for longer distances
perpendicular to the orientation axis of the selected cell than along its
orientation axis. Hence, we'll consider 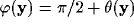 (see figure 2b),
even though, in the following, the effects of intracortical kernels with
orientations slightly different from the orthogonal one will be also
investigated.
(see figure 2b),
even though, in the following, the effects of intracortical kernels with
orientations slightly different from the orthogonal one will be also
investigated.


Next: The resultant receptive
Up: Linear analysis of
Previous: Superposition Assumption
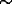 200:300
200:300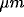 [73,104], thus leading to an
inhibitory action which is strongly local and uniformly distributed on the
horizontal plane. Such local inhibitory circuits are mainly involved in the
regulation of the gain of excitatory input
[32,33]. Much more interesting, for its functional implications, is long-range inhibition, evoked, often along
preferred directions, by clustered locations on the cortical surface.
The origin of this kind of inhibition can be related to
disynaptic activation of locally confined inhibitory interneurons through
long-range clustered branches of pyramidal cells
[81,94], and to the monosynaptic inhibitory action of basket cells which also have relatively long clustered axon collaterals, elongated in particular
directions and running tangentially for up to a millimeter from the soma
[63,64,65,67,104]. To model the consequences of this long-range inhibition, the kernel
[73,104], thus leading to an
inhibitory action which is strongly local and uniformly distributed on the
horizontal plane. Such local inhibitory circuits are mainly involved in the
regulation of the gain of excitatory input
[32,33]. Much more interesting, for its functional implications, is long-range inhibition, evoked, often along
preferred directions, by clustered locations on the cortical surface.
The origin of this kind of inhibition can be related to
disynaptic activation of locally confined inhibitory interneurons through
long-range clustered branches of pyramidal cells
[81,94], and to the monosynaptic inhibitory action of basket cells which also have relatively long clustered axon collaterals, elongated in particular
directions and running tangentially for up to a millimeter from the soma
[63,64,65,67,104]. To model the consequences of this long-range inhibition, the kernel 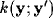 presents significant values only at a certain distance from
their centers, and along a direction forming a specific angle
presents significant values only at a certain distance from
their centers, and along a direction forming a specific angle 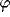 with
the horizontal axis.
with
the horizontal axis.


 ) the kernel will be
) the kernel will be
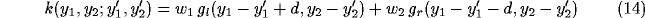
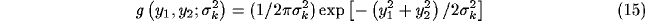
 ) along a direction
) along a direction  the kernel will be
the kernel will be
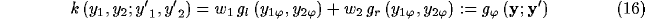
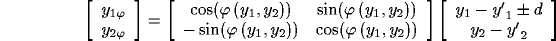
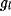 and the + sign for
and the + sign for 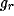 .
.
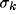 and their offset d are such that no
connections are established between two cells when their intracortical distance
is either too large or too small.
Moreover, the lateral spreading of interconnections can be characterized by
the angular bandwidth
and their offset d are such that no
connections are established between two cells when their intracortical distance
is either too large or too small.
Moreover, the lateral spreading of interconnections can be characterized by
the angular bandwidth 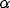 related to the half peak magnitude extension
of the kernel
related to the half peak magnitude extension
of the kernel
 (see
figure
(see
figure 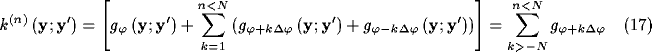
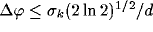 ,
,
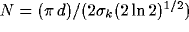 .
In this case the angular bandwidth results:
.
In this case the angular bandwidth results:
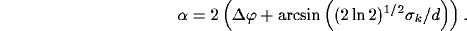


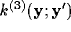 with
with 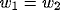 ,
, 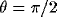 ,
, 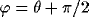 ,
, 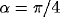 .
(a) 2D plot of the kernel. (b) Schematic representation of the spatial
extension of connections; the vertical thick line in the center
represents the orientation of the target cell. (c) Schematic mode of
operation on the
cortical plane: the marked cell (thick line) receives inhibition from
the cells (thin lines) in the shaded area.
.
(a) 2D plot of the kernel. (b) Schematic representation of the spatial
extension of connections; the vertical thick line in the center
represents the orientation of the target cell. (c) Schematic mode of
operation on the
cortical plane: the marked cell (thick line) receives inhibition from
the cells (thin lines) in the shaded area.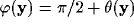 (see figure
(see figure