

Next: Analytical predictions of
Up: Results
Previous: Influence of the
Variations of the shape of the inhibitory kernel 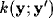 allow both (1) to assess the structural specificity of inhibition
schemata, and (2) to account for the observed variability in the
two-dimensional spatial organization of simple cell RFs.
Structural specificity is related to the anisotropic character of the
inhibitory kernel. Increasing the angle
allow both (1) to assess the structural specificity of inhibition
schemata, and (2) to account for the observed variability in the
two-dimensional spatial organization of simple cell RFs.
Structural specificity is related to the anisotropic character of the
inhibitory kernel. Increasing the angle 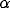 within which the recipient
cell gets its inhibition, the connection schema loses its specificity,
until, as
within which the recipient
cell gets its inhibition, the connection schema loses its specificity,
until, as 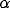 approaches
approaches  , inhibition arises from an annulus
around the center cell (see figure 5a, according to a ``circular inhibition'' schema
[123]. We verified, see figure 6a,
[92] that notwithstanding the isotropic and non-specific character of ``circular
inhibition'' schema, the resulting RFs still have specific and anisotropic
appearance, as pointed out in the recent study of Wörgötter and his
colleagues
[123]. In addition, for this type of inhibition, we observed that the central excitatory subregion is often
surrounded by an inhibitory ring of variable strength which provides RF
with a certain amount of end-stopping (i.e., sensitivity to the length of
the stimulus), that is a very common property of cells in the visual cortex
[9,28].
, inhibition arises from an annulus
around the center cell (see figure 5a, according to a ``circular inhibition'' schema
[123]. We verified, see figure 6a,
[92] that notwithstanding the isotropic and non-specific character of ``circular
inhibition'' schema, the resulting RFs still have specific and anisotropic
appearance, as pointed out in the recent study of Wörgötter and his
colleagues
[123]. In addition, for this type of inhibition, we observed that the central excitatory subregion is often
surrounded by an inhibitory ring of variable strength which provides RF
with a certain amount of end-stopping (i.e., sensitivity to the length of
the stimulus), that is a very common property of cells in the visual cortex
[9,28].
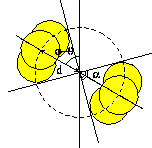
Figure 5: (click on the image to view a larger version)
Schematic representation of various inhibitory schemata. (a) circular inhibition; (b) anisotropic non-clustered inhibition; (c) asymmetric clustered inhibition, 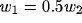 ; (d) slant (tilted) clustered inhibition.
; (d) slant (tilted) clustered inhibition.
Figure 6: (click on the image to view a larger version)
The resulting 2-D RF profiles together with their contour levels for a
cell in an iso-orientation domain subjected to the corresponding inhibitory
schemata in figure 5. The strength of inhibition b is fixed to 0.5.
Also in the case of ``circular inhibition'', long-range clustered
connections play a decisive role in endowing the resulting RF its periodic
appearance. To probe further into the function of long-range inhibition,
we conducted simulations with uniformly distributed inhibitory couplings that
have no skips and drop off uniformly with distance. The results showed that
non-clustered inhibition schemata, as the one depicted in
figure 5b, slightly improve feature sensitivity of
the resulting RF, providing it with two weak inhibitory sidebands, but fail
in generating periodic RFs, even for high values of b and when inhibition
occurs along a preferred direction (see figure 6b).
Real simple cell RFs present a broad variability of symmetry relationships
among field subregions
[24,26,27,40,61,62,93] that can be emulated only by introducing asymmetric or skewed inhibition kernels.
By example,
if 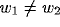 , inhibitory effect is spatially unbalanced (see
figure 5c) and the
resulting RFs exhibit still a periodical structure with continuous
phase shifts related to the ratio
, inhibitory effect is spatially unbalanced (see
figure 5c) and the
resulting RFs exhibit still a periodical structure with continuous
phase shifts related to the ratio 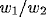 .
In figure 6c a RF with quasi-odd symmetry is shown.
Further realistic asymmetric behaviors, such as cartesian non-separability
(see figure 6d)
[61], can arise from inhibitory connections that do not extend exactly along the direction orthogonal to
the orientation preference of the cell (see figure 5d)
or from the joint effect of asymmetries in the inhibitory kernel and in the
underlaying orientation map.
.
In figure 6c a RF with quasi-odd symmetry is shown.
Further realistic asymmetric behaviors, such as cartesian non-separability
(see figure 6d)
[61], can arise from inhibitory connections that do not extend exactly along the direction orthogonal to
the orientation preference of the cell (see figure 5d)
or from the joint effect of asymmetries in the inhibitory kernel and in the
underlaying orientation map.


Next: Analytical predictions of
Up: Results
Previous: Influence of the
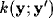 allow both (1) to assess the structural specificity of inhibition
schemata, and (2) to account for the observed variability in the
two-dimensional spatial organization of simple cell RFs.
Structural specificity is related to the anisotropic character of the
inhibitory kernel. Increasing the angle
allow both (1) to assess the structural specificity of inhibition
schemata, and (2) to account for the observed variability in the
two-dimensional spatial organization of simple cell RFs.
Structural specificity is related to the anisotropic character of the
inhibitory kernel. Increasing the angle 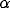 within which the recipient
cell gets its inhibition, the connection schema loses its specificity,
until, as
within which the recipient
cell gets its inhibition, the connection schema loses its specificity,
until, as 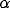 approaches
approaches  , inhibition arises from an annulus
around the center cell (see figure 5a, according to a ``circular inhibition'' schema
[123]. We verified, see figure 6a,
[92] that notwithstanding the isotropic and non-specific character of ``circular
inhibition'' schema, the resulting RFs still have specific and anisotropic
appearance, as pointed out in the recent study of Wörgötter and his
colleagues
[123]. In addition, for this type of inhibition, we observed that the central excitatory subregion is often
surrounded by an inhibitory ring of variable strength which provides RF
with a certain amount of end-stopping (i.e., sensitivity to the length of
the stimulus), that is a very common property of cells in the visual cortex
[9,28].
, inhibition arises from an annulus
around the center cell (see figure 5a, according to a ``circular inhibition'' schema
[123]. We verified, see figure 6a,
[92] that notwithstanding the isotropic and non-specific character of ``circular
inhibition'' schema, the resulting RFs still have specific and anisotropic
appearance, as pointed out in the recent study of Wörgötter and his
colleagues
[123]. In addition, for this type of inhibition, we observed that the central excitatory subregion is often
surrounded by an inhibitory ring of variable strength which provides RF
with a certain amount of end-stopping (i.e., sensitivity to the length of
the stimulus), that is a very common property of cells in the visual cortex
[9,28].





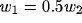 ; (d) slant (tilted) clustered inhibition.
; (d) slant (tilted) clustered inhibition.



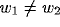 , inhibitory effect is spatially unbalanced (see
figure
, inhibitory effect is spatially unbalanced (see
figure 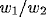 .
In figure
.
In figure