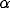 '', or complex, of the
form ``stimulus resembles shape prototype
'', or complex, of the
form ``stimulus resembles shape prototype 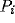 '') leads to the
emergence of a representation that is, in a sense, greater than the
sum of its parts.
'') leads to the
emergence of a representation that is, in a sense, greater than the
sum of its parts.


The complementary side of Locke's world view, echoed in
[19] --- the formation of complex ``ideas'' by associating
simple ones (those directly available in the sensory input) --- has
received recently stunningly direct experimental support in
Miyashita's results (see the Physiology of ... section). This and other
examples from low-level and high-level vision, in which lateral
connections turned out to be indispensable to the modeler, indicate
that a common functional principle may underlie the existence of
lateral connections in the cortex. I propose that the unifying
principle is associative formation of structured coarse-coded
representations. Given the computational power of lateral
information processing, it should not come as a surprise that
association of ideas (whether simple, of the form ``contrast
element C is present at orientation 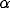 '', or complex, of the
form ``stimulus resembles shape prototype
'', or complex, of the
form ``stimulus resembles shape prototype 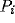 '') leads to the
emergence of a representation that is, in a sense, greater than the
sum of its parts.
'') leads to the
emergence of a representation that is, in a sense, greater than the
sum of its parts.
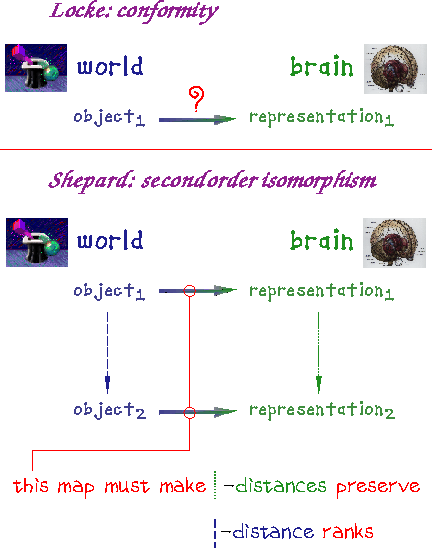
Figure 10: Lateral thinking in the
philosophy of representation. Locke's idea of representation
by covariation (that is, by a causal connection between the world
and the mind) has been criticized as incapable of providing a
sufficiently firm basis for veridical representation (see the
discussion in
[5]). Representation by
covariation, which appears to be the central tacit assumption
behind much of the contemporary brain science, becomes viable if
combined with Shepard's notion of ``second-order''
isomorphism
[6]. Shepard notes
that ``... the isomorphism should be sought --- not in the
first-order relation between (a) an individual object, and
(b) its corresponding internal representation --- but in the
second-order relation between (a) the relations among
alternative external objects, and (b) the relations among
their corresponding internal representations. Thus, although the
internal representation for a square need not itself be square, it
should (whatever it is) at least have a closer functional relation
to the internal representation for a rectangle than to that, say,
for a green flash or the taste of a persimmon''
[37]. Lateral links among object
representations may help to make second-order isomorphism work, as
argued in the Lateral Comparisons ... section.