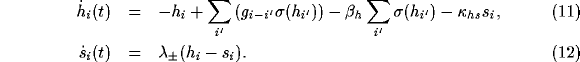
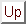
Generating a running blob can be achieved by delayed self-inhibition, which drives the blob away from its current location; the blob generates new self-inhibition at the new location. This mechanism produces a continuously moving blob (see Figure 3). The driving force and the recollection time as to where the blob has been can be independently controlled by their respective time constants. The corresponding equations are (cf. Equations 1 and 2):
The self-inhibition 
is realized by a leaky integrator with
decay constant 
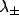. The decay constant has two different
values depending on whether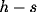 
is positive or negative. This
accounts for the two different functions of the self-inhibition.
The first function is to drive the blob forward. In this case
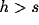and a high decay constant 
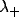is appropriate. The
second function is to indicate where the blob has recently been,
i.e., to serve as a memory and to repel the blob from regions
recently visited. In this case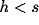 
and a low decay constant
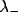is appropriate. For small layers, 
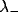should be
larger than for large ones, because the blob visits each location
more frequently. The speed of the blob is controlled by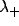 
and the coupling parameter 
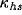. They may also change
the shape of the blob. Small values such as those used in our
simulations allow the blob to keep its equilibrium shape and drive it
slowly; large values produce a fast-moving blob distorted to a
kidney-shape.
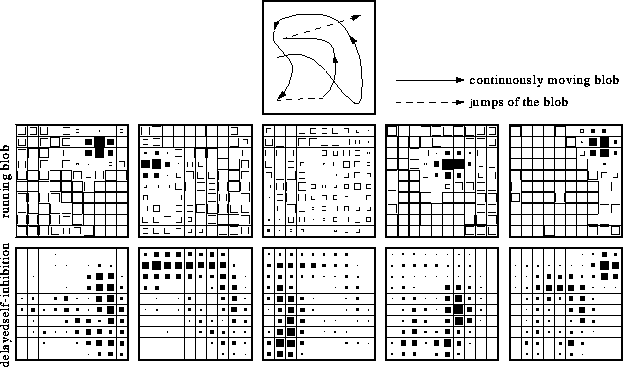
Figure 3: (click on the image to view a larger version) A sequence of layer states as
simulated with Equations 11 and
12. The activity blob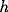 
shown in the middle row has a size of approximately six active nodes
and moves continuously over the whole layer. Its course is shown in
the upper diagram. The delayed self-inhibition 
, shown in the
bottom row, follows the running blob and drives it forward. One can
see the self-inhibitory tail that repels the blob from regions just
visited. Sometimes the blob runs into a trap (cf. column three) and
has no way to escape from the self-inhibition. It then disappears
and reappears again somewhere else on the layer. (The temporal
increment between two successive frames is 20 time units.)
