
A fundamental aspect of perception is to bind spatially separate sensory features to form coherent objects, essential for object identification, segmentation of different objects, and figure/ground segregation. Theoretical considerations point to the temporal correlation of feature detectors as a binding mechanism [1,42,62,64]. The temporal correlation theory [62] asserts that in the brain remote cells coding different sensory features are bound together if their temporal activities (such as firing patterns) show strong correlation. Thus, an object may be analyzed and represented by cell groups across different brain regions, generally consistent with known neurobiological findings [31]. As shown in von der Malsburg and Schneider [64], neural oscillations provide a natural way of implementing temporal correlation, whereby synchronized oscillators form an oscillator group to represent the common object, and groups desynchronized from each other represent different objects. More recently it was demonstrated that the cat visual cortex exhibits 30-60 Hz stimulus-dependent oscillations, and synchronization exists in spatially remote columns (up to 7 mm) which reflects global stimulus properties [13,24]. Later experiments further show that phase-locking can occur between the two striate cortices of the two brain hemispheres [14], between the striate cortex and the extrastriate cortex [15], and across the sensorimotor cortex [44].
Since the discovery of stimulus-driven oscillations and long-range synchronization in the visual cortex, many theoretical attempts have been made to interpret the phenomenon of global phase locking with no phase shift (to be called phase locking hereafter) [10,34,30,55,56]. Others have employed computational characteristics of temporal oscillations for solving problems of scene segmentation and figure/ground segregation [4,43,57,63], and associative memory [28,71]. Most of these models rely on an all-to-all connected oscillator network to reach synchronization (phase entrainment) across the network. A frequently used scheme is the phase model [4,30,55] which represents each oscillator by a sole phase variable and describes mutual coupling by an odd periodic function such as sine. The simplest form of the phase model can be defined as
where 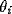 is the phase of oscillator i, and
is the phase of oscillator i, and 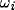 represents the internal
frequency and/or the external input. The systems of coupled phase models
have been extensively analyzed in mathematics and theoretical physics
(known as the X-Y models) literature
[11,16,33,36,47].
While global coupling readily yields phase locking, a system with only
local coupling does not seem to be able to generate global synchrony in
the presence of noise.
Although Sporns et al.
[56], Wilson and Bower
[73], and Chawanya et al.
[10] used local connections in simulating the experimental data,
their simulations only demonstrated correlation of a few oscillators and
their models do not seem to be capable of producing long-range synchrony.
An exception is the model by König and Schillen
[34] who simulated global
synchrony with local connections. Their model is based on delays between
an excitatory unit and an inhibitory unit to generate oscillations. In
particular, the model requires that the delay from the excitatory unit of
an oscillator X to the inhibitory unit of X
is on the same order as the
delay between the coupled oscillators, namely the delay from the excitatory
unit of X to the inhibitory units of all local oscillators that
X projects to.
represents the internal
frequency and/or the external input. The systems of coupled phase models
have been extensively analyzed in mathematics and theoretical physics
(known as the X-Y models) literature
[11,16,33,36,47].
While global coupling readily yields phase locking, a system with only
local coupling does not seem to be able to generate global synchrony in
the presence of noise.
Although Sporns et al.
[56], Wilson and Bower
[73], and Chawanya et al.
[10] used local connections in simulating the experimental data,
their simulations only demonstrated correlation of a few oscillators and
their models do not seem to be capable of producing long-range synchrony.
An exception is the model by König and Schillen
[34] who simulated global
synchrony with local connections. Their model is based on delays between
an excitatory unit and an inhibitory unit to generate oscillations. In
particular, the model requires that the delay from the excitatory unit of
an oscillator X to the inhibitory unit of X
is on the same order as the
delay between the coupled oscillators, namely the delay from the excitatory
unit of X to the inhibitory units of all local oscillators that
X projects to.
We consider it critically important to form synchrony using only local connections, in order to support useful computations, particularly segmentation, by neural oscillations. The reason is that long-range, all-to-all connections lose geometrical relationships among oscillators, important for perceptual grouping, thus leading to indiscriminate synchronization. This point will be emphasized in the Why Local ... section. This chapter describes a new model that can demonstrate stable long-range synchrony based on only local coupling in a network of neural oscillators. Based on plausible neural mechanisms, we use the model to simulate the experimental data of synchronous oscillations in the visual cortex. Also, we illustrate how such a network may be used to solve the engineering problem of scene segmentation. A preliminary version of this work has been presented previously [65,66]. This chapter largely follows the description in Wang [68]. In the postscript, we review most recent advances since Wang [68], and provide justifications of biological plausibility and discussions on the origin of synchronous oscillations in the visual cortex.