Experiments

The model consisted of an array of 192 × 192 neurons, and a retina of 24 × 24 ganglion cells. The circular anatomical receptive field of each neuron was centered in the portion of the retina corresponding to the location of the neuron in the cortex. The RF consisted of random-strength connections to all ganglion cells less than 6 units away from the RF center. The cortex was self-organized for 30,000 iterations on oriented Gaussian inputs with major and minor axes of half-width 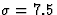$\sigma=7.5$and 1.5 , respectively. The training took 8 hours on 64 processors of a Cray T3D at the Pittsburgh Supercomputing Center. The model requires more than three gigabytes of physical memory to represent the more than 400 million connections in this small section of the cortex.

Orientation map organization

In the self-organization process, the neurons developed oriented receptive fields organized into orientation columns very similar to those observed in the primary visual cortex. The strongest lateral connections of highly-tuned cells link areas of similar orientation preference, and avoid neurons with the orthogonal orientation preference. Furthermore, the connection patterns of highly oriented neurons are typically elongated along the direction in the map that corresponds to the neuron's preferred stimulus orientation. This organization reflects the activity correlations caused by the elongated Gaussian input pattern: such a stimulus activates primarily those neurons that are tuned to the same orientation as the stimulus, and located along its length (Sirosh, Miikkulainen, and Bednar, 1996). Since the long-range lateral connections are inhibitory, the net result is decorrelation: redundant activation is removed, resulting in a sparse representation of the novel features of each input (Barlow 1990; Field 1994; Sirosh, Miikkulainen, and Bednar 1996). As a side effect, illusions and aftereffects may sometimes occur, as will be shown below.

Aftereffect simulations

In psychophysical measurements of the TAE, a fixed stimulus is presented at a particular location on the retina. To simulate these conditions in the model, the position and angle of the inputs were fixed to a single value for a number of iterations, rather than having a uniform random distribution as in self-organization. To permit more detailed analysis of behavior at short time scales, the learning rates were reduced from those used during self-organization, to 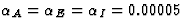$\alpha_A=\alpha_E=\alpha_I=0.00005$. All other parameters remained as in self-organization.

 

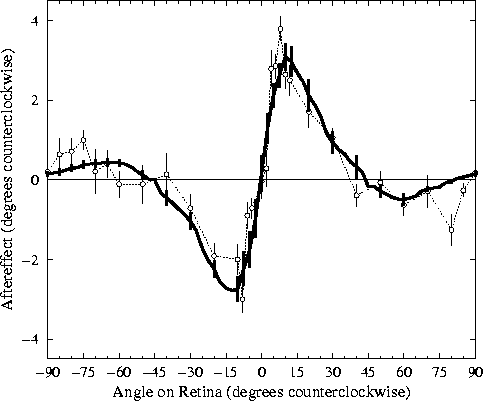
Figure 3: Tilt aftereffect versus retinal angle.

To compare with the psychophysical experiments, perceived orientations were compared before and after tilt adaptation. Perceived orientation was measured as a vector sum over all active neurons, with the magnitude of each vector representing the activation level, and the vector direction representing the orientation preference of the neuron before adaptation. Perceived orientation was computed separately for each possible orientation of the test Gaussian, both before and after adaptation. For a given angular separation of the adaptation stimulus and the test stimulus, the computed magnitude of the tilt aftereffect is the difference between the initial perceived angle and the one perceived after adaptation. Figure 3 plots these differences after adaptation for 90 iterations of the RF-LISSOM algorithm. For comparison, figure 3 also shows the most detailed data available for the TAE in human foveal vision (Mitchell and Muir, 1976).

The results from the RF-LISSOM simulation are strikingly similar to the psychophysical results. For the range 5° to 40°, all subjects in the human study (including the one shown) exhibited angle repulsion effects nearly identical to those found in the RF-LISSOM model. The magnitude of this direct TAE increases very rapidly to a maximum angle repulsion at approximately 10°, falling off somewhat more gradually to zero as the angular separation increases.

The results for larger angular separations (from 45° to 85°) show a greater inter-subject variability in the psychophysical literature, but those found for the RF-LISSOM model are well within the range seen for human subjects. The indirect effects for the subject shown were typical for that study, although some subjects showed effects up to 2.5°.

In addition to the angular changes in the TAE, its magnitude in humans increases regularly with adaptation time (Gibson and Radner, 1937). The equivalent of ``time'' in the RF-LISSOM model is an iteration, i.e. a single cycle of input presentation, activity propagation, settling, and weight modification. As the number of adaptation iterations is increased, the magnitude of the TAE in the model increases monotonically, while retaining the same basic shape of figure 3 (Bednar, 1997). The curve that best matches the human data was shown in figure 3.

Due to the time required to obtain even a single point on the angular curve of the TAE for human subjects, complete experimental measurements of the angular function at different adaptation times are not available. However, when the time course of the direct TAE is measured at a single orientation, the increase is approximately logarithmic with time (Gibson and Radner, 1937), eventually saturating at a level that depends upon the experimental protocol used (Greenlee and Magnussen, 1987; Magnussen and Johnsen, 1986). Figure 4 compares the shape of this TAE versus time curve for human subjects and for the RF-LISSOM model.

 

Figure 4: Direct tilt aftereffect versus time.

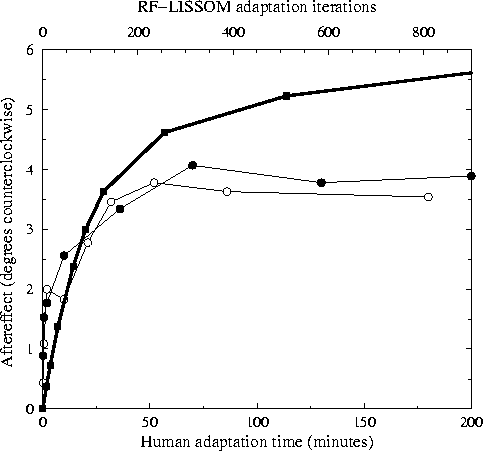The x axis for the RF-LISSOM and human data has different units, but the correspondence between the two curves might provide a rough way of quantifying the equivalent real time for an ``iteration'' of the model. The time course of the TAE in the RF-LISSOM model is similar to the human data. The TAE increases approximately logarithmically, but it does not completely saturate over the adaptation amounts tested so far. This difference suggests that the biological implementation has additional constraints on the amount of learning that can be achieved over the time scale over which the tilt aftereffect is seen.

How does the TAE arise in the model?

The TAE seen in figures 3 and 4 must result from changes in the connection strengths between neurons, since no other component of the model changes as adaptation progresses. Simulations performed with only one type of weight (either afferent, lateral excitatory, or lateral inhibitory) adapting at a given time show that the inhibitory weights determine the shape of the curve for all angles (Bednar, 1997). The small component of the TAE resulting from adaptation of either type of excitatory weights is almost precisely opposite the total effect. Although each inhibitory connection adapts with the same learning rate as the excitatory connections (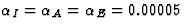$\alpha_I=\alpha_A=\alpha_E=0.00005$), there are many more inhibitory connections than excitatory connections. The combined strength of all the small inhibitory changes outweighs the excitatory changes, and results in a curve with a sign opposite that of the components from the excitatory weights.

In what way do the changing inhibitory connections cause these effects? During adaptation, we see that the response to the 0° adaptation line becomes gradually more concentrated towards the central area of the Gaussian pattern presented. This is because the inhibition between active neurons increases, allowing only the most strongly activated neurons to remain active after settling (equation 2). However, the distribution of active orientation detectors is centered around the same angle, so the same angle is perceived.

The response to a test line with a slightly different orientation (e.g. 10°) is also more focused after adaptation, but the overall distribution of activated neurons has shifted. Fewer neurons that prefer orientations close to the adaptation line now respond, but an increased number of those that prefer distant angles do. This is because inhibition was strengthened primarily between neurons close to the adaptation angle, and not between those which prefer larger orientations, greater than the 10° test line. The net effect is a shift of the perceived orientation away from the adaptation angle, resulting in the direct TAE.

In contrast, the response to a very different test line (e.g. 60°) is broader and stronger after adaptation. Adaptation occurred only in activated neurons, so neurons with orientation preferences greater than 60°are unchanged. However, those with preferences somewhat less than 60° actually now respond more strongly. During adaptation, their inhibitory connections with other active neurons, i.e. those that represent orientations close to the 0° adaptation line, became stronger. Since the sum of inhibition is constant for each neuron (equation 3), the connections to neurons representing distant angles (e.g. 60°) became weaker. As a result, the 60° line now inhibits them less than before adaptation. Thus they are more active, and the perceived orientation has shifted towards 0°. This indirect effect is therefore true to its name, caused indirectly by the strengthening of inhibitory connections. The RF-LISSOM model thus shows computationally that both the direct and indirect effects could be caused by activity-dependent adaptation of inhibitory lateral interactions.