Handwritten Digit Recognition Utilizing Evolved Pattern Generators

Vinod Valsalam, James A. Bednar, and Risto Miikkulainen

Self-organization of connection patterns within brain areas of animals begins prenatally, and has been shown to depend on internally generated patterns of neural activity. Such activity is genetically controlled and has been proposed to give the neural system an appropriate bias so that it can learn reliably from complex environmental stimuli. This idea is demonstrated here computationally using competitive learning networks for recognizing handwritten digits. The results demonstrate how training the network with patterns from an evolved pattern generator before training with the actual training set can improve learning performance by discovering the appropriate initial weight biases. This approach is expected to be useful in building complex artificial systems, such as the learning system of a robot with uninterpreted sensors and effectors.

Experimental Setup



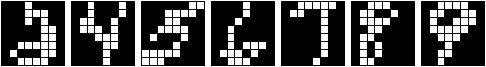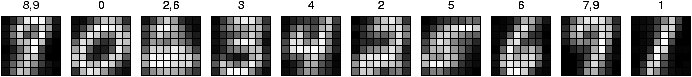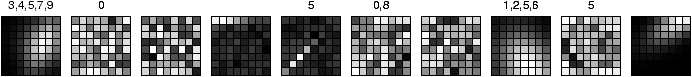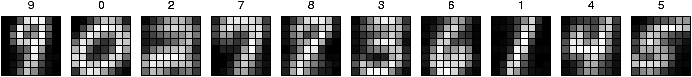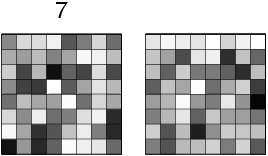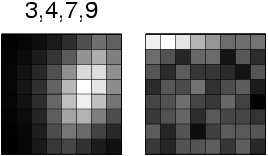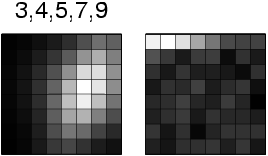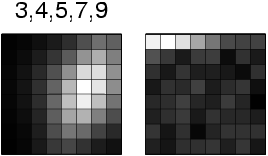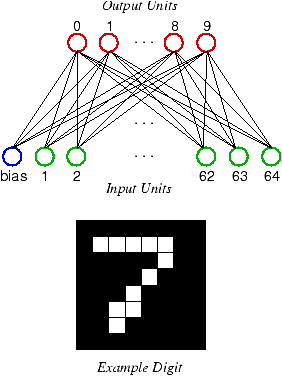
Figure 1: The architecture of the competitive learning network. The binary activations from the 8×8 input pattern consisting of 64 pixels are fed to the input units of the network, which also contains a bias unit. The 10 output units each correspond to a classification of the input as one of the 10 digits; the one with the highest activation is chosen as the answer of the network. During training, the weights of this unit are adjusted towards the input pattern, making that unit more likely to win similar patterns in the future.




Figure 2: Example inputs in the handwritten digit recognition domain. The original 39 × 39 gray-scale images from the NIST database were downsampled and thresholded to form a simple but challenging set of examples for the experiment.


Initial Network



Figure 3: Random weights of each output unit of the initial network. The weights are arranged in an 8×8 grid corresponding to the pixels in the input image. Lighter squares represent stronger weights. A digit on top indicates that this unit wins a large number of examples of that digit. The assignment of digits to units is uneven, indicating that this network is a poor classifier.


Unbiased Learning



Figure 4: Final weights for each output unit without prenatal biasing. Most of the weights have converged to a configuration that imitates the input digit patterns; however, some units represent a combination of digits (e.g. 7 and 9). This result demonstrates how competitive learning can get stuck in a local optimum when it does not start with an appropriate initial bias.


Biased Learning

Before looking at the network weight plots of the prenatal biasing approach, let us look at the patterns produced by the evolved pattern generator.


Figure 5: Patterns produced by the evolved pattern generator. The pattern generator consists of a set of oriented Gaussian patterns, each with a probability of generation shown on top of the pattern. These patterns tend to be simple and have no direct resemblance to digits. The weights resulting from prenatal training with such patterns are shown in Fig. 6(a). This biased network is then trained with digit examples to get the final recognition network (Fig. 6(b)). The classification performance of the final network is used as the fitness of the pattern generator in evolution.


[(a) Weights after prenatal training]


[(b) Final weights]


Figure 6: Weights for each output unit, trained prenatally with patterns shown in Fig. 5. Comparing the random weights network in Fig. 3 and weights after prenatal training (a), it is clear that only five of the ten units learn a significant bias. Yet, these biases are sufficient for postnatal training to perform better than without prenatal biasing — all digits are represented well by the final weight patterns (b).


How Does Biasing Help?

The most obvious way to establish an appropriate bias would be to separate each digit to a different unit as much as possible already in prenatal training, so that postnatal training would find it easier to complete the separation. However, this effect is typically not seen in the prenatal training phase: some units end up representing several different digit classes. How does such seemingly counterproductive initial bias make postnatal learning easier? The following animation makes this clear with an example showing how prenatal biasing helps disambiguate digits 7 and 9.
                 Prenatal biasing
                
                  
Training without prenatal biasing                Training after prenatal biasing
              
Digits 7 and 9 have several pixels in common, which results in the same unit learning both digits when the network is not biased. On the other hand, when the network is biased with the generated patterns, it is able to learn non-overlapping categories of 7 and 9. Prenatal training establishes a general bias on one of the units that matches several digits including 7 and 9, while another unit picks up a slight bias for 7. During postnatal learning, these biases allow the second unit to slowly become more and more specialized to digit 7, thus winning examples of that digit from the first unit. At the same time, the first unit keeps examples of digit 9 from interfering with the learning of digit 7 by the second unit. In the end, only digit 9 remains mapped to the first unit, while the other digits have been learned by other units in the network.

Conclusions

Encoding the bias in the pattern generator and transferring it to the network through learning has two advantages. First, the compact encoding of bias in the form of pattern generators allows evolution to be more efficient by restricting search to a small space compared to searching directly in the large space of network weight values. Second, establishing the bias using a learning process makes the system flexible and easily adaptable to new training data because the bias is not hardwired by design. These characteristics make the biasing technique presented here potentially useful for building complex artificial systems.

References

[1]
Vinod Valsalam, James A. Bednar, and Risto Miikkulainen. Constructing good learners using evolved pattern generators. In H.-G. Beyer et al., editors, Proceedings of the Genetic and Evolutionary Computation Conference, GECCO-2005, pages 11–18. New York: ACM, 2005.
This document was translated from LATEX by HEVEA.